Un vector es una herramienta matemática, generalmente utilizada en geometría y física, que permite llevar a cabo cálculos y operaciones.
En física, un vector es un segmento de recta en el espacio que presenta módulo (también llamado longitud) y dirección (u orientación). Los vectores se representan gráficamente con una flecha y ayudan a describir magnitudes vectoriales.
Las magnitudes vectoriales son representadas a través de un vector porque no pueden ser determinadas por un único número real, sino que es necesario conocer su dirección y sentido. Por ejemplo: velocidad, desplazamiento. Esto las distingue de las magnitudes escalares, que solo requieren de un número y de cierta unidad de medida para ser definidas, por ejemplo: la presión, el volumen, la temperatura.
En matemática, los vectores son los elementos de un espacio vectorial. Esta noción es más abstracta, ya que en muchos espacios vectoriales no puede definirse el vector a partir de módulo y dirección, por ejemplo: vectores en espacios de dimensión infinita. La representación que se utiliza para representar a un vector en un espacio de “n” dimensiones es: v= (a1, a2, a3,…an)
Los vectores pueden sumarse o restarse entre sí para dar origen a un nuevo vector resultante, o bien multiplicarse por un valor escalar, vectorial o mixto.
- Ver además: Trabajo mecánico
Elementos de un vector
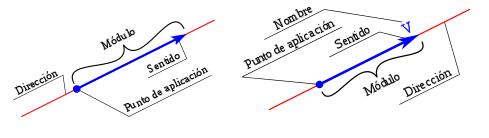
Para definir un vector de manera completa, se deben especificar tres características que distinguen a un vector de otro:
- Módulo. Está determinado por la longitud o largo del segmento de recta.
- Dirección. Está determinado por la orientación que presenta la recta en el plano.
- Sentido. Está determinado por el origen y el extremo final del segmento de recta.
Tipos de vectores
Pueden distinguirse diversas clases de vectores según las características que presenten y la relación que tengan con otros vectores:
- Vectores unitarios. Vectores cuyo módulo es igual a 1.
- Vectores libres. Vectores que no se encuentran aplicados en ningún punto en particular.
- Vectores deslizantes. Vectores cuyo punto de aplicación se desliza a lo largo de la recta de acción.
- Vectores fijos (o vectores ligados). Vectores que están aplicados en un punto particular.
- Vectores colineales. Dos o más vectores que actúan en una misma recta de acción.
- Vectores concurrentes (o vectores angulares). Dos o más vectores cuyas direcciones pasan por un mismo punto, formando un ángulo al cruzarse las semirrectas.
- Vectores paralelos. Dos o más vectores que actúan sobre un cuerpo rígido con líneas de acción paralelas.
- Vectores opuestos. Vectores que tienen la misma dirección y el mismo módulo, pero que presentan sentidos contrarios.
- Vectores coplanarios. Vectores cuyas rectas de acción se encuentran situadas en el mismo plano.
- Vectores resultantes. Dado un sistema de vectores, es el vector que produce el mismo efecto que todos los vectores componentes del sistema.
- Vectores equilibrantes. Vector con la misma magnitud y dirección que el vector resultante, pero que tiene sentido opuesto.
Los vectores en la vida cotidiana
Los vectores son muy utilizados en muchos ámbitos de la vida cotidiana porque permiten conocer magnitudes y representarlas a partir de su módulo, sentido y dirección.
Suelen usarse para:
- Marcar recorridos. Todos los recorridos que realiza un individuo, tanto caminando como en algún medio de transporte, involucran a uno o más vectores. Estos vectores son los que otorgan sentido al recorrido porque delimitan distancias y dirección. Esta función es muy usada por los GPS para marcar caminos o recorridos desde un punto del plano hacia otro.
- Medir distancias. Los vectores permiten medir la distancia desde un punto a otro y calcular cuánto se tardará en hacer el recorrido según la velocidad, el medio de transporte, entre otras variables
- Practicar deportes. Los vectores son las magnitudes que intervienen durante la práctica de muchos juegos y deportes, ya que determinan la dirección y el sentido que el individuo dará a un elemento, como puede ser una pelota. Los vectores permiten calcular distancias y realizar lanzamientos a otros jugadores o encestar. La importancia de los vectores en este ámbito se aprecia muy claramente en deportes como el billar, en el que el jugador utiliza parte de un segmento para guiar el curso de la pelota.
- Jugar videojuegos. Los vectores son muy utilizados a la hora de posicionar y medir elementos dentro de un espacio. Esto permite que en los videojuegos el jugador pueda mover y direccionar objetos o personajes desde un punto del plano hacia otro.
- Realizar el control aéreo. Los vectores se usan en el ámbito aéreo para dar una dirección y sentido a la aeronave y para que los pilotos puedan dirigirla desde un determinado punto hacia otro.
- Conducir un medio de transporte. Los vectores son indispensables para trazar y delimitar orientaciones y direcciones, por lo que son utilizados en el transporte para que el conductor conozca la ruta y el recorrido.
- Calcular fuerzas y aceleraciones. Los vectores permiten calcular la velocidad de objetos en movimiento y también sus aceleraciones. Además, se usan para obtener otros tipos de medidas, como los lados de una edificación.
- Diseñar caminos y carreteras. Los vectores son usados en el ámbito de la arquitectura, el diseño y la construcción para llevar a cabo edificaciones y construcciones como edificios, carreteras y puentes.
- Mover objetos. Conocer las distancias y el sentido de los vectores permite que el individuo pueda manipular elementos (y a su propia persona) para lograr determinados fines. Esto es lo que permite que una persona pueda llevarse una taza de té a la boca o que direccione el paraguas según la orientación de la lluvia.
Vectores en dos y en tres dimensiones
Los vectores pueden representarse en espacios de dos dimensiones (“x”, “y”) o de tres dimensiones (“x”,”y”,”z”). En cualquier caso, los vectores pueden ser definidos mediante sus coordenadas en cada uno de los ejes.
En el caso de un espacio de dos dimensiones, un vector cualquiera puede ser definido como: v=(vx,vy). Los términos entre paréntesis son las coordenadas sobre los ejes “x” e “y”.
Por otro lado, en un espacio de tres dimensiones, un vector se define como: v=(vx,vy,vz). Se agrega una coordenada más para indicar la coordenada sobre el eje “z”.
Representación gráfica de los vectores
Los vectores se representan de forma general recurriendo a un plano de dos o tres dimensiones.
- En primer lugar, se grafica la recta soporte o dirección, sobre la que pueden existir varios vectores, dibujando un segmento de recta que surge del origen.
- En segundo lugar, se marca la longitud del vector, el cual está determinado por el módulo (a mayor módulo, mayor longitud de la semirrecta), y que está dirigido a una dirección o punto de aplicación (razón por la cual se dibujan los vectores como flechas que apuntan hacia la dirección en cuestión).
- Por último, se escribe el nombre del vector sobre el punto de aplicación.
Ejemplos de magnitudes vectoriales en física
- Densidad
- Velocidad
- Desplazamiento
- Fuerza normal
- Aceleración
- Campo eléctrico
- Campo magnético
- Campo gravitatorio
- Peso
- Velocidad angular
- Aceleración angular
- Fuerza de rozamiento
Ejemplos de vectores en matemática
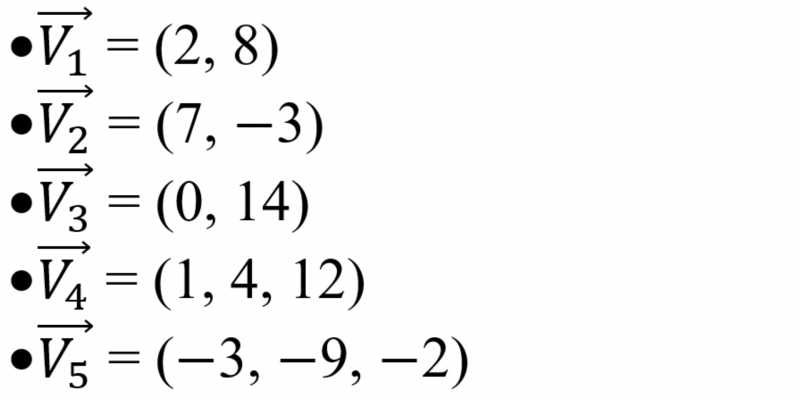
Sigue con:
¿Te fue útil esta información?
Sí No¡Genial! gracias por visitarnos :)