Ejemplos de
Ángulo agudo, obtuso, recto y llano

El encuentro entre dos líneas o semirrectas siempre da lugar a la formación de un ángulo. En general se habla de ángulos para hacer referencia a la trigonometría plana, es decir la que corresponde al encuentro entre semirrectas que no tienen una forma curva sino que es una línea. Por ejemplo: ángulo aguado, ángulo obtuso, ángulo recto.

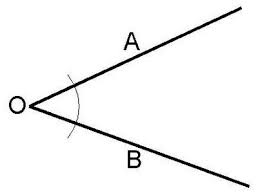
El punto en el que las dos semirrectas se tocan se denomina vértice, y es allí el nacimiento del ángulo: se trata de una entidad que no tiene una delimitación física sino que está allí, a partir del vértice y hasta que las dos semirrectas finalizan o bien cambian de forma.

Es frecuente que se busque establecer relaciones de similaridad o de diferencia entre los ángulos. Cuando dos ángulos tienen el vértice y un lado en común se los denomina consecutivos, mientras que cuando tienen en común al vértice pero los lados se continúan en forma opuesta (es decir, el vértice es común pero el ángulo se forma del otro lado) se los denomina opuestos por el vértice: los ángulos opuestos por el vértice siempre tienen la misma amplitud, y entonces dan lugar a dos pares de ángulos de igual amplitud.

Esto sucede porque el ángulo no podrá tener una amplitud infinita sino que como máximo será la del giro completo, 360 ° (grados), 400 ^g (grados centesimales) o 2π radianes. Los ángulos que se combinan dando la totalidad del giro se llaman suplementarios, mientras que los que lo hacen generando un cuarto de un giro se denominan complementarios.

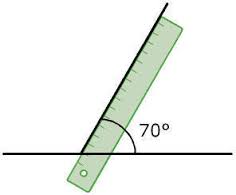
La cuestión de las amplitudes de los ángulos es el fundamento matemático de la trigonometría, y siempre fue indispensable en materia de las aplicaciones matemáticas de la realidad: todo lo que tiene que ver con construcciones de arquitectura e ingeniería se vale de este tipo de procedimientos. La herramienta elemental para la medición de la amplitud de un ángulo es el transportador, que no comprende la totalidad del giro sino que la mitad de él.

La medición que usa es la de los grados, por lo que el máximo que podrá captar son los 180°. El modo de utilizar la herramienta es colocar el lado recto del transportador sobre uno de los lados del ángulo, y verificar el valor angular del otro lado según la escala del transportador. Ese será el ángulo, indistinto del largo de los lados. De acuerdo a la amplitud de los lados, aparece la clasificación más habitual de la medida de los ángulos.

Ejemplos de ángulo agudo, obtuso, recto y llano

Ángulos agudos

Son los que tienen una amplitud menor a los 90°, es decir al cuarto de giro. Los triángulos equiláteros (los que tienen todos sus lados iguales) siempre están compuestos por tres ángulos de 60°, es decir tres ángulos agudos.

1. 
2. 
3.  
4. 
5. 

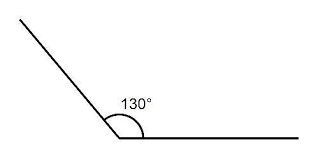
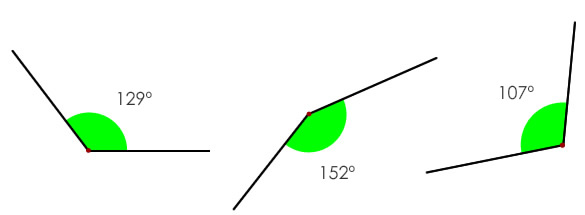
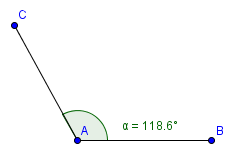
Ángulos obtusos

Son los que tienen una amplitud mayor a los 90°, pero menor a los 180°. Si alguna de las dos semirrectas se prolonga más allá del vértice, estará acompañado por uno agudo y darán lugar a los 180°. Si las dos semirrectas se prolonga más que el vértice, habrán dos pares de ángulos opuestos por el vértice para sumar 360°.

1. 
2. 
3. 
4. 
5. 

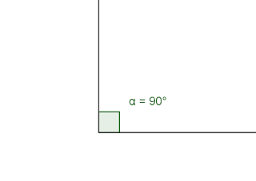
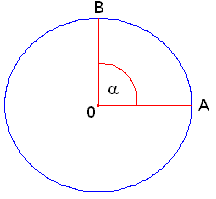
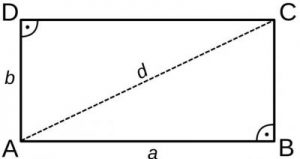
Ángulos rectos

Son los que miden exactamente 90°. La simbología que suele hacerse para expresar esto es el ángulo en forma de cuadrado en vez de en forma de círculo. Todos los cuadrados y los rectángulos poseen cuatro ángulos de este tipo, por lo que en su interior suman 360°.

1. 
2. 

3. 

4. 

5. 

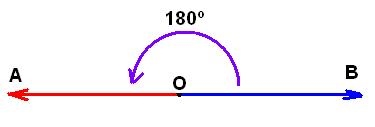
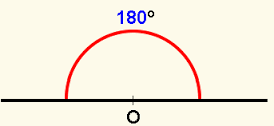
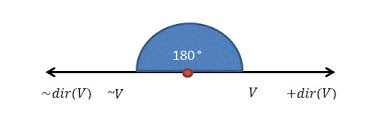
Ángulos llanos

Son los que tienen una amplitud de 180°, por lo que representan la mitad del giro. Esto significa que, a simple vista, los lados conforman una única semirrecta que se continúa: cualquier recta, si se la piensa de este modo, está compuesta por infinitos vértices de ángulos de 180°. Un buen ejemplo del ángulo llano es el que generan las agujas del reloj cuando la hora es las 6:00.

1. 
2. 

3. 

4. 
5.